Оказалось, что коэффициент интеллекта (IQ), который раньше считали врождённым, вполне реально прокачать тренировкой! Это доказано современными исследованиями. Звучит вдохновляюще, правда? Поэтому знаменитый тест «Матрицы Равена», который проверяет уровень интеллекта, можно использовать не только по прямому назначению. Он может стать тем самым упражнением для мозга, которое способно реально  ПОВЫСИТЬ УРОВЕНЬ IQ!  И действует это на всех – и на детей, и на взрослых. В статье подробно расскажем, как и почему это работает. Итак, за дело!

Используем тест «Матрицы Равена» для повышения коэффициента интеллекта (IQ): тренировки с профессором

О чём расскажем: 

• Совершенно новая реальность
• Секрет получения максимума при прохождении  теста «Матрицы Равена»
• Пол-ответа плюс пол-ответа
• Гении любят удивлять
• Тайная хитрость профессора Равена
• Самое важное понятие для уровня С
• Мир, упакованный в задачи

Совершенно новая реальность

Джон Равен, создатель теста на проверку уровня интеллекта, был выдающимся ученым своего времени и профессором. Он создал серию рисунков из фигур – так, что в каждом рисунке одного пазла не хватает. Задача: выбрать из предложенных вариантов рисунок, который идеально  впишется в рисунок. Это, вкратце, и есть знаменитый тест «Матрицы Равена». Однако такие задания можно использовать еще и как идеальную тренировку для интеллекта. Почему идеальную? Да потому что профессор Равен отобрал для своих заданий материал, представляющий МАКСИМАЛЬНУЮ ЭФФЕКТИВНОСТЬ.

На уровне А  мы имели дело с единым пространством, в котором не хватало одной детали и нужно было её восстановить. На уровне В мы работали с парами, устанавливая сходства и различия между участниками каждой пары. И вот теперь пришла пора разобраться с  уровнем С.

На уровне С мы оказываемся в совершенно новой реальности. Не единое полотно, не пары, а … клетчатая шахматная доска. Хотя и совсем небольшая – 3 на 3 клетки. Я могла бы назвать то, с чем нам придется иметь дело на этом уровне, таблицей. В таблице 3 строки и 3 столбца. Но это немного скучновато. «Маленькая шахматная доска» – самое то:

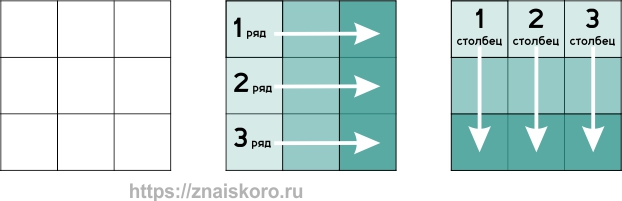
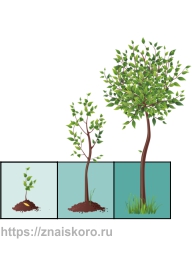Каждая клетка на этой доске заполнится фигурами. И конечно, эти фигуры не случайны. Они меняются по определенным правилам. Это похоже на сказочную историю, где рисунки начинают расти и развиваться прямо на ваших глазах. Истории рассказываются слева направо (по рядам)  или сверху вниз (по столбцам). При этом каждая фигура постепенно становится сложнее, словно взрослеет и обзаводится всё большим количеством деталей.

Лёгкая разминка

В самых простых матрицах уровня С это движение происходит по одному маршруту. Например, только сверху вниз, как в задании С1:

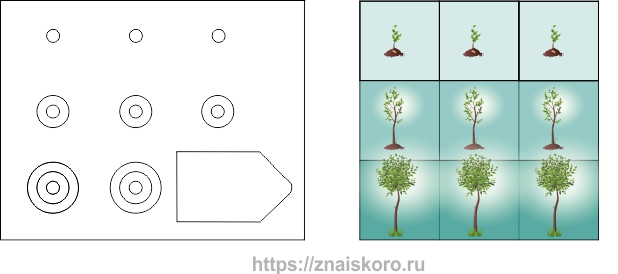
Понимая это, мы просто выбираем нужное дерево для того, чтобы красиво продолжить ряд. Это – самая простая задача цикла С из теста матрицы Равена. Такая простота нужна для того, чтобы дать нашему мозгу сигнал: вот таким будет поле, и  здесь надо будет выращивать фигуры. Выращивать – это значит от клетки к клетке, постепенно добавлять к тому, что посажено в начале, всё больше элементов и сложностей. Основной принцип: что-то посадили, и оно стало изменяться.

И сразу со второй картинки, без раскачки, начинается настоящая работа шахматиста-садовода. На этом поле изменения идут сразу в двух направлениях: вверх-вниз и вправо-влево. Что посадили? Допустим, маленький подсолнух. И он стал постепенно увеличиваться в размере, расти от первой клетки к третьей. И слева направо, и сверху вниз.

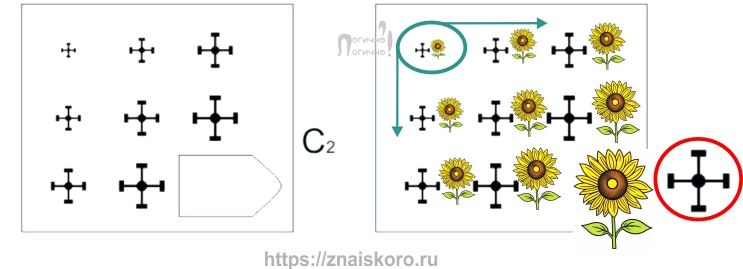
Поэтому – внимание! – в последней клетке, в конце всего этого поля, нас ждет самый большой подсолнух. Подсолнух-гигант. Интересно то, что в этой матрице исходный маленький подсолнух нам уже больше никогда не встретится. Точно так же, как самый большой подсолнух нам еще никогда не встречался. Запомним это хорошенько:

Первая, начальная клетка теста «матрицы Равена» — такая же неповторимо-уникальная, как и последняя, конечная.

Ну а для других клеток всегда может найтись на нашем поле двойник. Из всех подробностей в этом задании изменяется (добавляется) только размер: он  постоянно увеличивается. Таким образом, мы имеем на одном поле самую маленькую фигуру (начальную) и  самую большую. Эту большую фигуру мы и должны подыскать из числа вариантов. И тут важно, конечно, чтобы не подвел глазомер, который бывает очень важен и в логике.

Секрет получения максимума при прохождении  теста «Матрицы Равена»

Вашей сверхзадачей на все последующие 10 картинок станет роль садовника-исследователя: внимательно присмотреться к каждому ряду клеток-грядок и понять скрытые законы роста растений-фигур. Что же прибавляется в каждом следующем ряду? Какие происходят изменения? Необходимый спойлер в этом месте. Изменения эти – не хаотичны, и будут они происходить по нескольким основным направлениям. Одно из них уже нам известно, это – размер.  

В матрице  Равена № 3 садим картошку: сама по себе она не меняется, зато постоянно и постепенно меняется ее количество. Была одна – затем две – и потом три. Дойдя до конца этого картофельного поля, в последней клетке мы увидим уже целый мешок картошки. А не одну большую картофелину (как в случае с подсолнухом). Там менялся размер – здесь меняется количество.

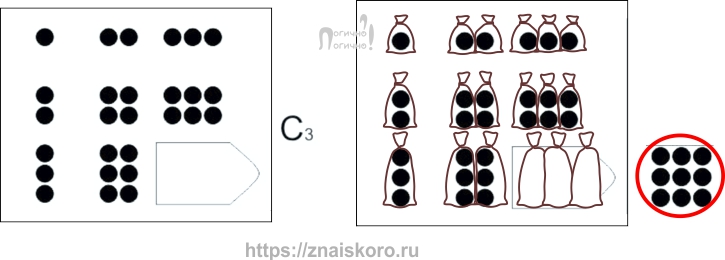
Однако небольшая хитрость поджидает нас и здесь. Сначала мы имели дело с простым счетом: одна картошка – две картошки – три картошки. Но потом начинается счет не картошками, а мешками. Но по точно такому же принципу: один мешок – два мешка – три мешка. И главное здесь – следить за тем, что мы считаем именно мешки. То есть, считаем повторяющиеся мерки (по принципу умножения). Такой счет – мерками – нам еще пригодится в одном из самых сложных заданий раздела.

В пятой картинке теста «Прогрессивные матрицы Равена» мы оказываемся на ромашковом поле. Здесь тоже – игры с количеством. Но вот не самих ромашек, а их лепестков. Слева направо добавляется по одному лепестку (1-2-3), и сверху вниз – тоже (1-2-3). В конце поля, как мы уже и привыкли, получаем максимум, которого еще не было на поле и который мы постепенно, пошагово вырастили практически с нуля,  – полную ромашку.

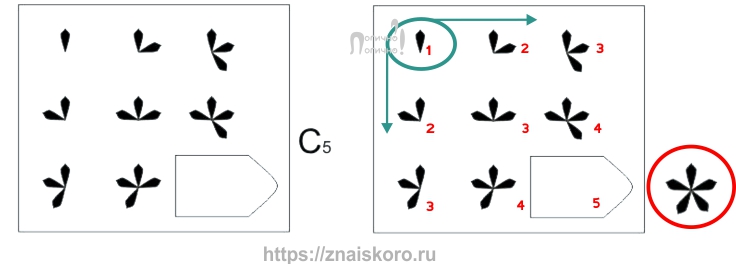
Если завести перечень изменений, то на этом этапе он станет уже вот таким:

1. размер
2. количество (фигур или их элементов)

Этот перечень будет фиксировать не только задумки профессора Равена. Здесь будет отражаться наш растущий практический опыт.

Куда девать растущий опыт?

Привычка мысленно вести перечень изменений великолепно пригождается, если дело касается логических заданий.  Большинство заданий в рисунках на поиск закономерностей неизменно сводятся к умению находить сходства и фиксировать различия  между фигурами.

Например, в этом задании из серии «продолжи последовательность» нужно проанализировать 7 предложенных вариантов. Проанализировать – это для нас, учеников профессора Равена, уже не пустой звук! Это значит — началась игра-охота  в «найди общее и отметь разное».

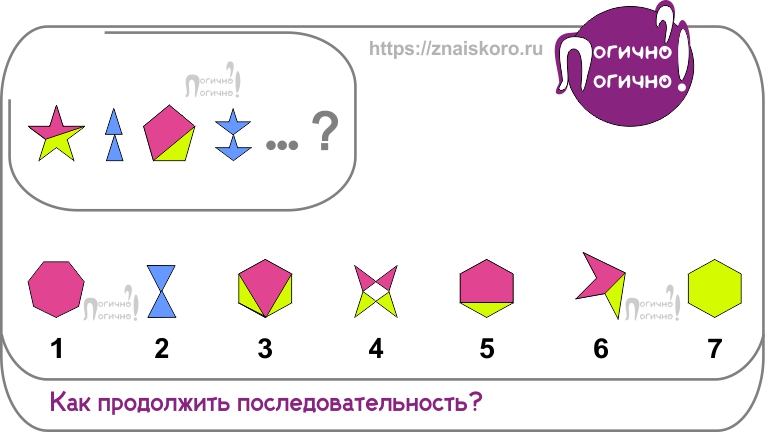
Не правда ли, отличный  тренажер для развития динамического внимания и наблюдательности!  Просто внимание – это одно. А вот динамическое внимание похоже на свет прожектора, мгновенно переключающегося между деталями рисунка! Оно выделяет важное, отбрасывая лишнее, позволяя увидеть общую картину и уловить направление происходящих изменений. У тех, кто  успешно справляется с матрицами Равена, динамическое внимание уже на уровне прожектора! И прожектор этот с большой скоростью выхватит верный ответ из целой цепочки похожих фигур. А вот если динамическое внимание пока еще на уровне непрочно мерцающей свечки, то надо срочно поднабрать практики – и тогда картина непременно исправится!

Больше идей – меньше сомнений

В следующем задании  надо разгадать секрет превращений голубой медузы в двухцветный шар. А потом проделать то же самое с ожидающей своей очереди розовой медузой. Всё, что происходит в этом задании, подчинено логике и легко разгадывается с её помощью. Поэтому-то такие задания называются логические преобразования:

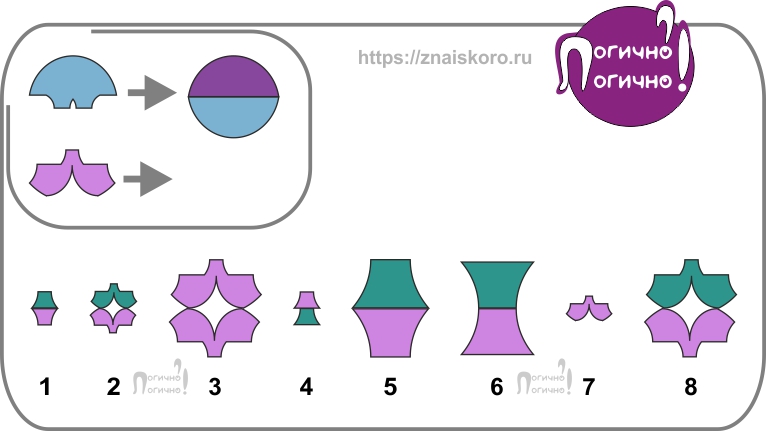
Перед нами — компания из четырех загадочных фигур. Одну из них мы должны вернуть на своё законное место вместо знака вопроса. И эта компания очень напоминает маленькое поле по выращиванию изменений, с которым мы сталкиваемся, когда проходим тест матрицы Равена! Но только в матрицах уровня С поле большое, девятиклеточное. А здесь — совсем крошечное, всего только из четырех клеток.  Однако подход от этого не меняется: если у решальщика есть навык искать и сравнивать – с ответом всё будет хорошо.

Каждый, кто прошел до этого момента логическую школу профессора Равена, поняли одну важную вещь: чтобы разгадать секрет рисунка, надо всего лишь увидеть то, что объединяет фигуры… и одновременно заметить, чем они друг от друга отличаются! Ну а остальное – дело практики. Чем больше такой увлекательной практики, тем острее глаз и быстрее скорость реакции!

Пол-ответа плюс пол-ответа

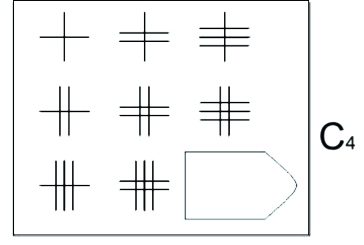Но вернёмся в увлекательный мир прогрессивных матриц Равена. Тем более, что в задании № 4 — немного запутанная картина. И именно здесь начинаются первые «сбои» и долгие размышления.

Мы уже привыкли к тому, что рисунки растут и развиваются прямо на наших глазах. Самая простая фигура в виде крестика – как всегда, вверху-слева. Постепенно крестик становится сложнее и обзаводится всё большим количеством деталей-палочек. Их так много, этих палочек, что от них рябит в глазах. И мы понимаем:  в последней клетке поля мы должны возвести целый забор из этих палок. Но вот каким будет этот забор?

И вот тут-то начинается самое интересное! Мы должны найти общую деталь, объединяющую весь ряд. Раньше мы фокусировались на различиях (был большой – стал маленький; был один – стало два и т.д.).  Ну а теперь будем искать подобие. Для этого – планомерно пропалываем ряды один за другим и фиксируем сходство:

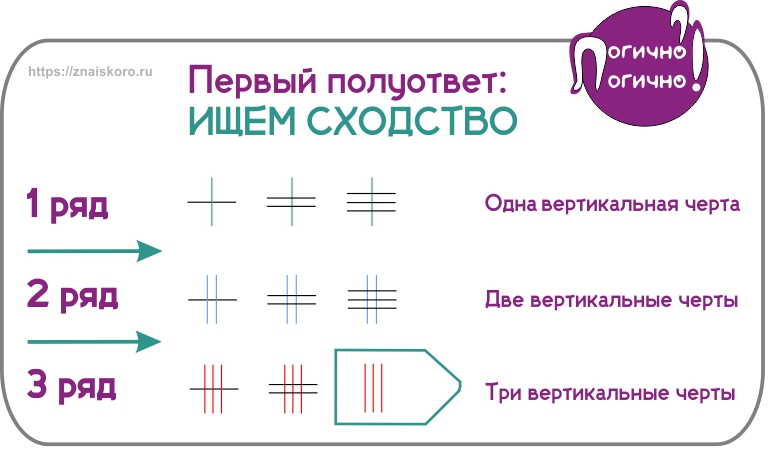
Общее у всех фигур этого ряда – три  вертикальные линии. Именно их мы увидим в правильном варианте. Пол-ответа найдено.

Идём за второй половиной ответа и для этого анализируем колонки клеток. Вопрос при этом не меняется: что общего в столбце?

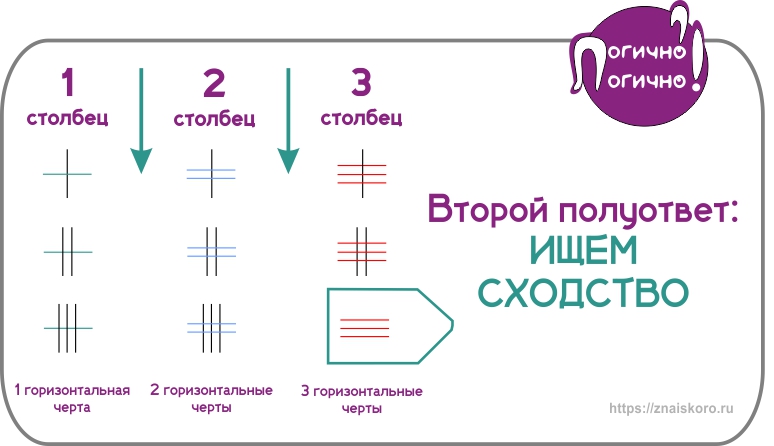
Складываем наши полуитоги: три вертикальные линии плюс три линии. Вот и готов наш забор. Под каким там он номером находится в вариантах ответов? Всё предельно понятно!

Гении любят удивлять

Ну и Равен не был бы Равеном, если бы  не  любил играть на противоположностях. Что ж, гении любят удивлять. Мы привыкли на нашем поле всё выращивать и увеличивать. Однако в шестой задаче уровня С получаем обратную операцию. В случае с ромашкой мы всё время добавляли ей элементы-лепестки, а теперь, похоже, будем отнимать. Так же последовательно и методично – но отнимать. Поэтому в крайней нижней клетке у нас получится не самая роскошная фигура, а самая куцая.

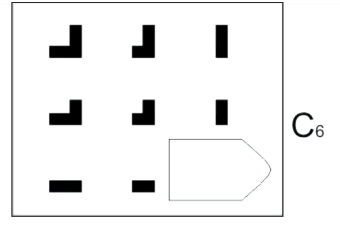
Попытаемся пробиться к правильному ответу на тест матрицы Равена через анализ рядов. (Хотя можно анализировать и столбцы).  Отличная основа для анализа — хорошая и забавная история. Сюжетность, между прочим, — отличный прием для решения логических задач. Статья, в которой истории помогают найти логическую закономерность, так и называется: «Самые интересные задачи». 

История про исчезающие стулья

Допустим, хозяин кафе купил в магазине отличный стул. Но посетителей в кафе было так много, что со временем стул поизносился. Да так, что часть сидения отвалилась. До поры до времени хозяин этого не замечал. Посетители продолжали кое-как сидеть на этом стуле. Но настал момент, когда отпала оставшаяся часть сидения. Тут уж хозяин не смог этого не заметить – потому что от стула осталась только спинка. Хоть спинка и была совершенно целая, но проку от неё – никакого!

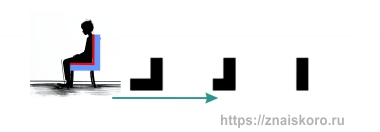
Второй ряд: хозяин пошел в магазин покупать новый стул. Такого же точно не было, но был другой, с небольшой спинкой. Хозяин  купил что было – и поставил в кафе. Прошло время — результат тот же. Спинка цела – сидение отвалилось.

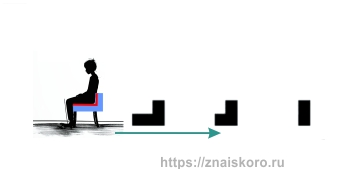
Третий ряд: денег на постоянную покупку некачественных стульев, видимо, уже было жалко. И хозяин решил, что вполне сгодится вместо стула обычный табурет. Но, увы, с табуретом история повторилась. Сначала сидение табурета укоротилось, а потом и вовсе… Исчезло? Ну вряд ли совсем исчезло —  табуреты просто так из жизни не исчезают, даже если на них очень часто и очень подолгу сидеть. Просто табурет так укоротился, что стал непригодным для сидения. Что осталось от табурета? Вот для ситуации самый подходящий ответ:

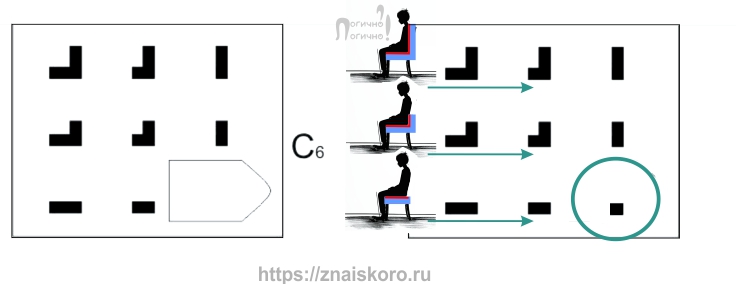
Только что мы показали, как абстрактные фигуры можно увидеть через творческие образы. И этот прием здорово работает! Это полезно не только для логики: воображение развивает креативность и умение мыслить нестандартно. Как подойти к теме логического творчества для совсем маленьких детей – описано в статье «Что такое хорошая логическая задача для дошкольников».

В качестве вывода по этой интереснейшей матрице стоит сказать очень важную вещь. Раньше изменения коснулись сначала количества фигур, а потом их элементов. Точно так же изменения стали происходить сейчас с размером – но не фигур, а элементов. А это, скажу я вам,  – очень хитрая вещь.

1. размер (фигур или их элементов)
2. количество (фигур или их элементов) 

Тайная хитрость профессора Равена

На одиннадцатом шаге нас ждет вроде бы понятная задача с уменьшением количества элементов. Но ход-то – одиннадцатый! А мы знаем, что в тесте Равена сложность заданий постепенно, но неуклонно возрастает. И если задача расположена  в конце – это значит, профессор Равен запечатал туда какую-то тайную хитрость. По сравнению с картошками, конечно.

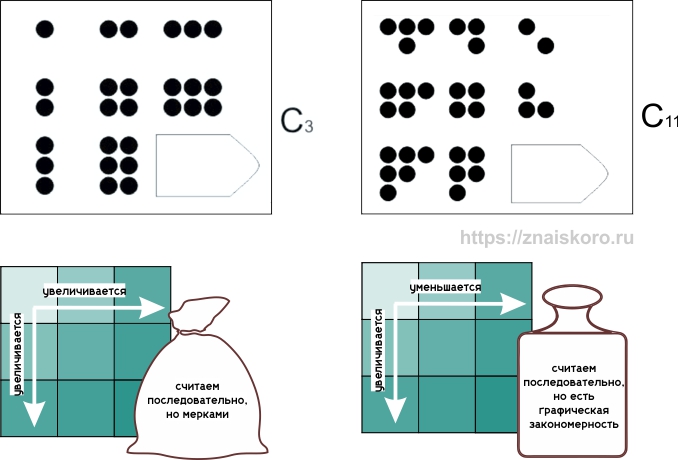
Итак, мы видим, что количество точек изменяется. В более раннем и легком третьем задании оно и в столбцах, и в рядах только увеличивалось. А теперь количество точек уменьшается в рядах, но зато увеличивается в столбцах. Смотрим на последний ряд: было шесть картошек, потом пять, ну и в конце… четыре — уменьшение. Проверяем на всякий случай по последнему столбцу: было две картошки, потом три, потом – четыре: увеличение.

Хоть так считай, хоть эдак – нужны четыре картошки. Беда в том, что вариантов с четырьмя картошками – слишком много. И некоторые торопливые решальщики хватают что-то первое попавшееся, не ожидая подвоха.  Главное, мол, количество. А  между тем,  в  этом задании  есть серьезный «утяжелитель» в виде графической закономерности. Что это значит? То, что картошки-точки отпадывают от своих чётко сформированных кучек или добавляются к ним не как попало. А в соответствии с какой-то логикой. Поэтому важно не просто убрать какую-нибудь любую картошку, чтобы их стало четыре. Важно убрать так, чтобы и картошек стало четыре, и чтобы рисунок всей кучки изменился строго в соответствии с закономерностью.

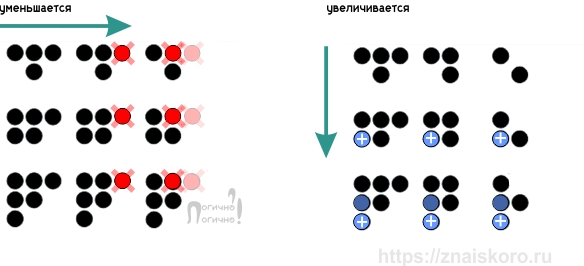
По рисунку видно: если мы получаем  фигуру уменьшением количества точек, то за один ход исчезает по одной точке справа (и сверху). А если мы получаем фигуру с помощью увеличения количества точек, то за каждый ход прибавляется по одной фигуре слева (и снизу). Результат, кстати, – одинаковый. Так что можно использовать любой из этих способов.

Самое важное понятие для уровня С

На седьмом ходу появляется кое-что принципиально новое и очень важное.

Вспомним наш основной перечень изменений. Начиная с этого момента он снова уточнился:

1. размер
2. количество
3. положение элементов (!)

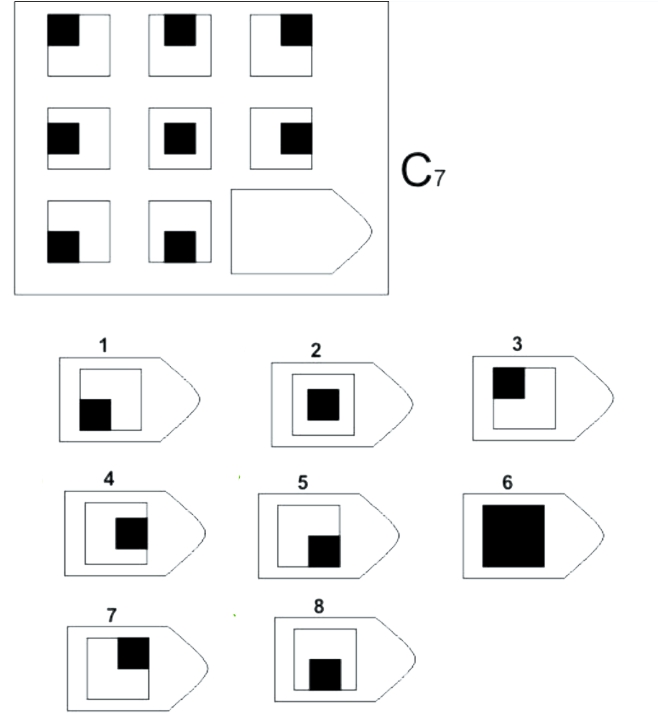
Черный квадрат меняет своё положение от ряда к ряду и от столбца к столбцу. Как всегда, пробежимся по рядам в поиске сходства.

Сходство – очень важное понятие для уровня «С» теста «Матрицы Равена». Надо научиться находить и использовать сходство фигур в рядах и столбцах.

Итак, в первом ряду чёрные квадраты живут наверху. В среднем ряду – посередине. Ну и понятно по такой логике, что в нижнем ряду все  квадраты спустятся вниз. На картинке, которую мы ищем, мы увидим черный квадрат где-то внизу. Но до ответа еще далеко: у нас три  варианта, подходящие под это описание. Это первый вариант, пятый и восьмой.

Что ж, поищем сходство в вертикальных рядах. В левом ряду все квадраты – слева. В центральном ряду – в центре. Ну и в правом ряду (который нам предстоит закончить) – справа. Соединяем все добытые несложными наблюдениями данные: нам нужна фигура, где черный квадрат внизу и одновременно справа. Такой есть! Записываем ответ: 5. Система складывания воедино двух полуответов – в действии!

Такой же алгоритм действий – в задании № 9:

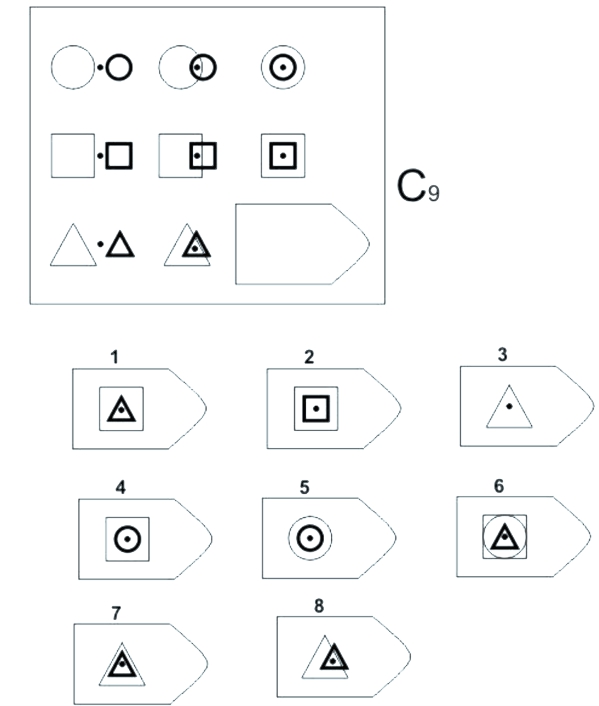
Пройдемся по рядам и отметим сходство фигур в каждом ряду. 1 ряд – все круги, 2 ряд – все квадраты, 3 ряд – все треугольники. Значит, нам нужен треугольник – это и есть первый полуответ. Теперь точно так же пройдемся по колонкам. 1 колонка – в каждой клетке фигуры рядом, но порознь. 2 колонка – в каждой клетке фигуры начали сближаться. Они как бы «взялись за руки». 3 колонка – фигуры слились, теперь у них – общий центр. Это второй полуответ. Объединяем два полуответа: нам нужен рисунок из треугольников, в котором все фигуры соединены вместе. И такой, конечно, быстро нашёлся – это номер 7.

Мир, упакованный в задачи

Джон Равен не просто разработал тест — он открыл новый мир, управляемый законами интеллекта и опыта. Здесь важны не только логика, но также скорость и динамическая наблюдательность — искусство моментально видеть скрытые связи, предугадывать последствия и избегать ошибочных путей.

Представьте: словно искусный серфер, ловко скользящий по волнам, опытный  логик свободно ориентируется в потоке задач, извлекая открытия из хаоса форм и изображений. Ведь для настоящего серфера океанская волна — тренажёр мастерства, удовольствие и самовыражение одновременно. То же самое справедливо и для интеллектуального серфинга! Миру логических испытаний нужны постоянные тренировки, как телу необходимы упражнения. Только тренируя интеллект, мы обретаем силу, уверенность и радость познания.

Почему-то существует мнение, что к тесту на айкью Равена нельзя или не надо готовиться. Однако интеллект требует развития, как мышцы требуют тренировок. Без усилий невозможно раскрыть истинный потенциал своего разума. Поэтому подготовка к тестам необходима и полезна, ведь именно она помогает превратить сложности в победы и испытать радость от собственных достижений!

Отлично подходят для логической тренировки задания из серии «Логично? Логично!», прокачивающие динамическую наблюдательность:

• Разнообразные
• Яркие
• Эксклюзивные
• Созданные на основе матриц Равена и многолетней педагогической практики
• Всевозрастные, разбитые на уровни
• С подробным объяснением решения.

Регулярная практика подобного рода повышает общую эффективность восприятия и принятия решений, улучшает скорость реакции и способствует формированию гибкого подхода к решению сложных интеллектуальных задач – таких, какие предлагает нам  тест «Матрицы Равена».

Читать ещё:

Какими могут быть математические головоломки для маленького Эйнштейна?

Интересные, нестандартные и правильные  задачи для дошкольников  с забавным героем отлично стимулируют умственное развитие.

Таблица умножения и её тренажер: миф о скорости

Развертки куба с логическим подходом

Рекомендую обратить внимание — эти задания гарантировано вдохновят вас на развитие логического мышления и интеллектуальных способностей!